Statistical Approaches to Machinery Problem Solving 
In today’s complex industrial landscape, machinery plays a crucial role in production and operations. However, machinery can encounter various problems that lead to downtime, inefficiencies, and increased operational costs. Statistical approaches offer powerful tools for problem-solving in this domain, enabling engineers and managers to identify issues, analyze data, and implement effective solutions. This comprehensive overview explores the principles, methodologies, and applications of statistical approaches to machinery problem-solving.
- Introduction to Statistical Approaches
1.1 The Importance of Data in Machinery Management
Data is central to effective machinery management. As machines operate, they generate vast amounts of data related to performance, maintenance, and operational conditions. Analyzing this data can reveal patterns, identify anomalies, and inform decision-making processes.
1.2 Statistical Tools and Techniques
Statistical approaches encompass a range of tools and techniques, including:
- Descriptive Statistics: Summarizing and describing data characteristics.
- Inferential Statistics: Drawing conclusions and making predictions based on sample data.
- Regression Analysis: Modeling the relationship between variables to predict outcomes.
- Statistical Process Control (SPC): Monitoring and controlling processes to ensure they operate at their full potential.
- Design of Experiments (DOE): Planning experiments to understand the effects of various factors on a response variable.
- Descriptive Statistics
2.1 Overview
Descriptive statistics provide a way to summarize and describe the main features of a dataset. Common measures include:
- Mean: The average value of a dataset.
- Median: The middle value when data is sorted.
- Mode: The most frequently occurring value.
- Standard Deviation: A measure of the amount of variation or dispersion in a set of values.
2.2 Application in Machinery Problem Solving
Descriptive statistics can help identify baseline performance levels of machinery. For instance:
- Performance Monitoring: Analyzing the average runtime or output of a machine to establish benchmarks.
- Quality Control: Understanding the distribution of product dimensions or defects to identify quality issues.
2.3 Case Example
In a manufacturing plant, descriptive statistics were used to monitor the production output of a milling machine over several months. By calculating the mean and standard deviation of the output, the plant manager could determine whether the machine was operating consistently and identify periods of underperformance.
- Inferential Statistics
3.1 Overview
Inferential statistics allow for making inferences about a population based on a sample. This involves hypothesis testing and confidence intervals.
3.2 Application in Machinery Problem Solving
Inferential statistics are useful for:
- Hypothesis Testing: Determining whether observed differences in machinery performance are statistically significant.
- Quality Control: Inferring the overall quality of a production batch based on a sample inspection.
3.3 Case Example
A factory experiences a sudden increase in defect rates. Using inferential statistics, the quality control team collects a sample of products from the production line and conducts hypothesis testing. They find that the defect rate is significantly higher than the historical average, prompting an investigation into potential causes.
- Regression Analysis
4.1 Overview
Regression analysis is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. It helps in predicting outcomes and understanding the influence of various factors.
4.2 Application in Machinery Problem Solving
Regression analysis can be applied in various scenarios:
- Predictive Maintenance: Modeling the relationship between machine operating conditions and failure rates to predict when maintenance should be performed.
- Performance Optimization: Understanding how changes in operational parameters (like speed or temperature) affect output quality.
4.3 Case Example
A manufacturing facility uses regression analysis to model the relationship between the temperature of a machine and the quality of the finished product. By analyzing historical data, they determine that certain temperature ranges correlate with higher defect rates, leading to adjustments in the cooling system.
- Statistical Process Control (SPC)
5.1 Overview
Statistical Process Control (SPC) is a method of quality control that uses statistical methods to monitor and control processes. It focuses on identifying variations in processes that may lead to defects or failures.
5.2 Key Tools in SPC
- Control Charts: Graphical representations that show how a process varies over time. Common types include:
- X-bar and R Charts: Used for monitoring the mean and range of a process.
- p-Charts: Used for monitoring the proportion of defective items in a sample.
- Process Capability Analysis: Evaluating how well a process meets specified limits or tolerances.
5.3 Application in Machinery Problem Solving
SPC can be implemented to:
- Monitor Machinery Performance: Regularly track performance metrics to identify trends and variations.
- Identify Root Causes of Problems: Use control charts to detect when a process goes out of control, prompting investigation.
5.4 Case Example
In a bottling plant, SPC is used to monitor the fill levels of bottles. Control charts reveal that fill levels are occasionally exceeding the upper control limit, leading to overfilling and increased costs. The plant manager investigates the filling machine and discovers a calibration issue, which is promptly resolved.
- Design of Experiments (DOE)
6.1 Overview
Design of Experiments (DOE) is a structured approach to experimentation that allows for the simultaneous evaluation of multiple factors and their interactions. It helps in understanding how different variables affect outcomes.
6.2 Application in Machinery Problem Solving
DOE can be used to:
- Optimize Processes: Test different operational parameters (e.g., speed, temperature, feed rates) to find the optimal settings for machinery.
- Investigate Failures: Understand the factors contributing to machinery failures by systematically varying conditions and observing outcomes.
6.3 Case Example
A company uses DOE to explore the impact of different lubrication types and application methods on the lifespan of machine bearings. By conducting a series of experiments, they identify the optimal combination that significantly increases bearing life, reducing maintenance costs.
- Implementing Statistical Approaches
7.1 Data Collection
The first step in implementing statistical approaches is effective data collection. This involves:
- Identifying Key Metrics: Determine which performance indicators (e.g., downtime, output quality) are relevant to machinery performance.
- Establishing Data Sources: Utilize machine sensors, operational logs, and maintenance records to gather data.
7.2 Data Analysis
Once data is collected, statistical analysis should be performed:
- Cleaning and Preparing Data: Remove outliers and ensure data integrity.
- Choosing Appropriate Techniques: Select the right statistical methods based on the objectives (e.g., descriptive statistics for summary, regression for prediction).
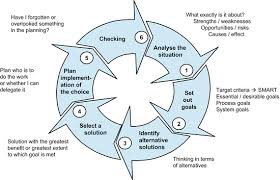
7.3 Interpretation and Decision-Making
Statistical analysis provides insights that need to be interpreted:
- Communicating Results: Present findings in a clear and actionable format for stakeholders.
- Making Informed Decisions: Use statistical insights to guide machinery management decisions, such as scheduling maintenance or modifying operational parameters.
- Case Studies in Statistical Problem Solving
8.1 Case Study: Automotive Manufacturing
An automotive manufacturing plant faced challenges with high defect rates in welded components. The quality control team implemented statistical process control (SPC) to monitor welding parameters. By analyzing data through control charts, they identified that variations in welding temperature were linked to increased defects. Adjustments were made to the welding process, resulting in a 25% reduction in defects over six months.
8.2 Case Study: Food Processing Industry
A food processing facility was experiencing inconsistent product quality. The management team applied regression analysis to explore the relationship between processing temperature, time, and product quality. The analysis revealed optimal processing conditions that maximized quality while minimizing processing time. This led to a 15% increase in overall product quality and a 10% reduction in processing costs.
- Challenges and Limitations
9.1 Data Quality Issues
The effectiveness of statistical approaches depends on the quality of the data collected. Inaccurate, incomplete, or biased data can lead to misleading results.
9.2 Complexity of Machinery Systems
Machinery systems are often complex, with many interacting components. This complexity can make it difficult to isolate variables and understand their effects fully.
9.3 Resource Constraints
Implementing statistical approaches may require additional resources, such as training personnel, investing in software tools, or acquiring data collection technologies.
- Future Trends in Statistical Approaches
10.1 Integration of Big Data and Machine Learning
As the volume of data generated by machinery increases, integrating big data analytics and machine learning into statistical approaches will enhance predictive capabilities and provide deeper insights.
10.2 Real-Time Analytics
Advancements in sensor technology and data processing will enable real-time analytics, allowing for immediate responses to identified issues and further optimizing machinery performance.
10.3 Enhanced Decision Support Systems
Future statistical tools are likely to incorporate advanced decision support systems that leverage AI and machine learning to assist in making informed machinery management decisions.
- Conclusion

Statistical approaches to machinery problem-solving offer powerful methodologies for identifying, analyzing, and addressing issues in industrial operations. By leveraging tools such as descriptive statistics, regression analysis, SPC, and DOE, organizations can enhance machinery performance, reduce downtime, and improve overall operational efficiency.
As technology continues to advance, integrating statistical methods with emerging data analytics and machine learning will further enhance the ability to solve machinery-related problems, leading to more resilient and efficient industrial systems. Adopting these approaches will be essential for organizations aiming to thrive in a competitive marketplace.

